Malandragem: como cientistas manipulam a estatística em suas pesquisas

Temos visto vários ataques à ciência. Entre os vários motivos pelo qual isso acontece, mudanças constantes de resultados de pesquisa científica acabam causando ceticismo entre o público leigo, principalmente quando a pesquisa influencia decisões pessoais ou governamentais.

Comer ovo faz bem ou faz mal? Beber uma taça de vinho por dia é salutar ou danoso para a expectativa de vida? Um caso emblemático foi a recomendação da aspirina diária que, hoje em dia, é considerada potencialmente danosa. É natural que uma pessoa conclua que, haja vista tamanha inconstância, a ciência não seja mais que um palpite.

A constante revisão de resultados anteriores, porém, é um resultado intencional da comunidade. Cientistas costumam replicar, refinar, aprimorar os estudos e é nesse processo que as mudanças de conclusões acontece.

Cientistas, inclusive, costumam revisitar não somente resultados, mas também métodos utilizados. Recentemente, a revista The American Statistician, publicada pela Associação Americana de Estatística, dedicou um exemplar inteiro revisitando a forma como cientistas utilizam ferramentas estatísticas em pesquisas científicas.

A crítica é focada no fato de que cientistas, às vezes, são capazes de produzir conclusões errôneas por utilizar essas ferramentas sem compreensão adequada, ou de forma antiética. As sugestões apontadas podem, portanto, afetar profundamente a forma como pesquisadores interpretam dados e aumentar a qualidade e robustez de novos estudos científicos.

Significância estatística

Um estudo científico quer responder perguntas, e para isso, mede ou observa um fenômeno para obter uma conclusão. Para formar uma boa observação científica e evitar conclusões espúrias, cientistas repetem diversas vezes o experimento ou observação sobre o fenômeno estudado e acumulam medições.

Mas por causa do número enorme de dados, isso não é fácil de manipular mentalmente. Para poder fazer uma análise útil, cientistas buscam aglutinar todos os dados coletados a um número menor de dados de fácil uso. Para isso, cientistas podem utilizar métodos estatísticos.

Para ilustrar o processo, eu vou usar um exemplo retirado de um artigo meu, estudando "impedância" em circuitos biológicos. Na figura abaixo, eu busquei comparar o comportamento de dois sistemas diferentes: um ilustrado pela curva preta e outro pela curva vermelha. Cada curva representa uma extrapolação de nove pontos, e cada um desses pontos foi obtido a partir de três observações distintas. A posição de cada ponto é a média das três observações. Cada ponto tem também uma margem de incerteza indicada pela barra vertical. Essa barra vertical também é conhecida como "intervalo de confiança."

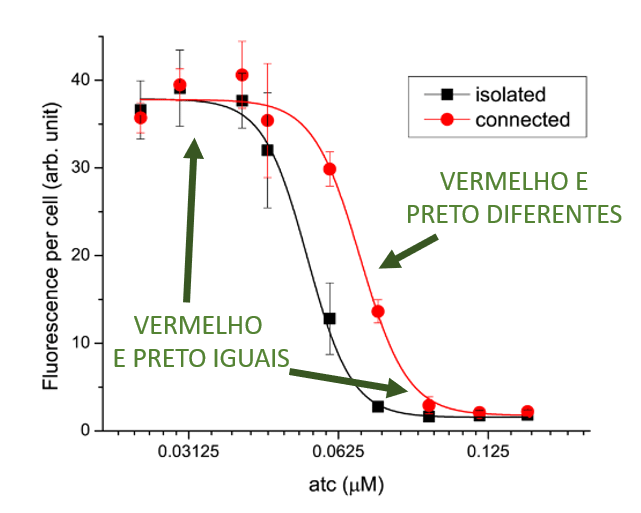
Olhando para o gráfico, podemos dizer que a curva vermelha e a curva preta são muito semelhantes nos quatro pontos à esquerda e nos três pontos à direita, uma vez que os intervalos de confiança se cruzam. Já os dois pontos do meio são diferentes, uma vez que os intervalos de confiança estão bem separados.

Um cientista diria que, nessa região do meio, as duas curvas são estatisticamente diferentes (diferença estatisticamente significante), enquanto nas outras regiões as duas curvas são estatisticamente iguais (diferença estatisticamente insignificante).

Uma outra forma de medir a significância em um estudo é o uso de testes estatísticos –justamente o alvo da discussão corrente. Esses testes tentam avaliar a probabilidade de que uma observação acontece por conta de uma hipótese específica ou se é produto de ruído puro (hipótese nula).

Por exemplo: vamos supor que um cientista notou que, depois de uma chuva, a grama em seu jardim cresceu. O cientista formulou então a hipótese de que a chuva causou o crescimento da grama.

Para testar a hipótese, o cientista observou que ao longo de um ano, todas as chuvas cauaram o crescimento da grama e assim concluiu que sua hipótese estava correta. Mas o cientista não foi diligente o suficiente para anotar o que acontece depois que não chove. É possível que a grama esteja crescendo todos os dias! Nesse caso, a hipótese nula é que a grama cresce, mas não por causa da chuva.

O valor de p

Testes estatísticos, como o teste de Fisher ou o teste t de Student, costumam produzir um coeficiente que indica a significância da hipótese em relação à hipótese nula, em vista dos dados. O limite estatístico é conhecido na literatura como valor de p (p-value).

Por exemplo, o cientista acima, depois de coletar dados sobre o efeito da grama na chuva, pode fazer um teste estatístico e comparar o coeficiente obtido (valor de p) com um limite (0.05, 0.005) para descobrir se o efeito da chuva na grama é significante (p< 0.05, p< 0.005).

Esses testes, porém, são vulneráveis a manipulação. Um exemplo de malandragem é o p-hacking, uma situação em que um pesquisador levanta um número enorme de dados, faz testes estatísticos para encontrar distinções estatisticamente significantes e formula uma hipótese a partir desse resultado.

O p-hacking é ruim, pois ele acaba invertendo a lógica da relação entre hipótese e teste e, dessa forma, acaba por exagerar a causalidade. O que é pior: o p-hacking acidental pode ocorrer mesmo sem malícia por parte do pesquisador se ele não entender conceitualmente como o teste estatístico, a hipótese e as observações estão relacionadas!

Um outro problema do uso do valor de p é que ele foca na distinção entre a hipótese proposta, dado o conjunto de observações, e só. Um resultado de insignificância não nega a hipótese, pois é possível que o problema seja na qualidade das medições.

Usando o exemplo da grama, vamos supor que a grama cresça 1 cm em dias com chuva, e 0,5 cm em dias que não chove. Se o nosso amigo cientista-jardineiro usar uma régua em uma escala de centímetros, o teste estatístico não vai mostrar significância, mesmo sendo a chuva responsável por dobrar a o crescimento!

Por outro lado, o valor de p não diz o quão importante a hipótese é. Vamos supor que a grama cresça 1 cm em dias com chuva e 0,99 cm em dias sem chuva, precisamente. O nosso amigo cientista-jardineiro, com um paquímetro e cuidado, vai obter um valor de p bem pequeno. Mas essa diferença de 0,01 cm importa? Não há teste estatístico que possa responder essa pergunta.

A direção sugerida pelos editores da publicação é a que pesquisadores compreendam melhor o que os testes dizem e o que o eles não dizem, e sejam mais cuidadosos no desenho de experimentos e no tratamento de dados, que sejam transparentes na publicação de resultados e que sejam tolerantes a resultados inesperados.

Essas sugestões são extremamente bem vindas. Nesses tempos em que a politização e polarização desafiam a credibilidade de cientistas e da ciência como um todo, o aumento da qualidade do desenho experimental, o uso responsável de ferramentas de análise e a maior transparência na divulgação de pesquisas melhorariam a robustez dos resultados.